
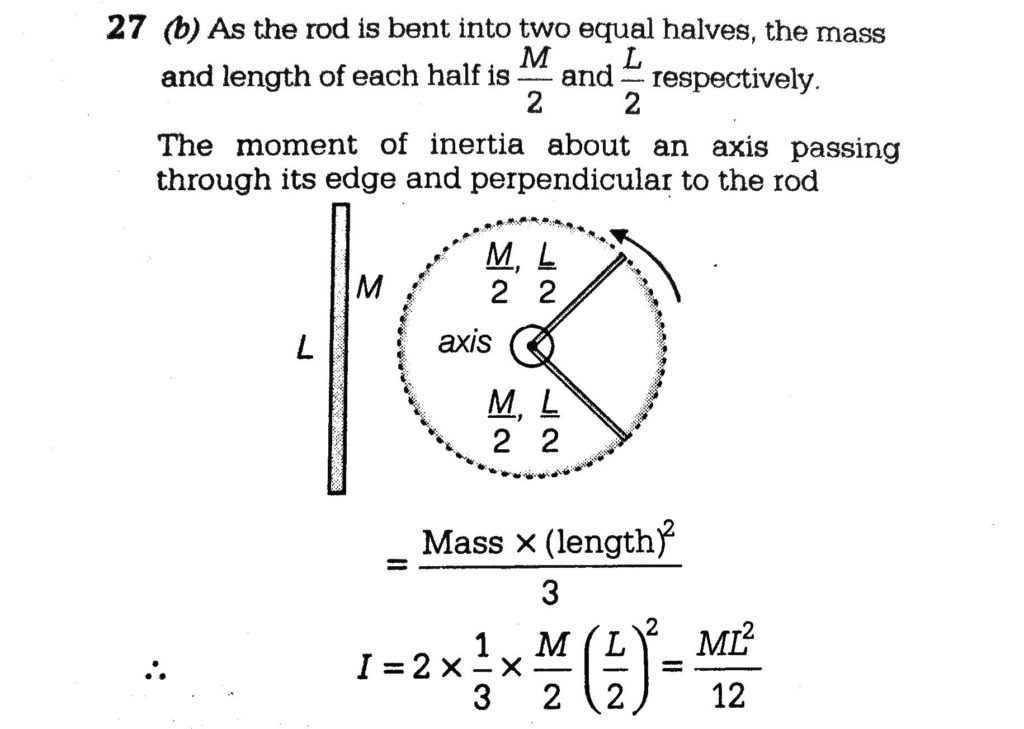
Since the torque you apply is related to the angular acceleration by τ = Iα, for a given applied torque, the greater the moment of inertia, the smaller the angular acceleration. These moments are roughly in a ratio of 1:10:20. As noted in 28.27 – Roll cylinders down incline, the moment of inertia for a cylinder of uniform mass distribution is (1/2) MR 2, and for a hoop it is MR 2. As discussed in 28.24 – Angular acceleration and 28.30 – Waggle rods with different moments of inertia, the moment of inertia, I, for an object is the sum of the products of all its mass points and the squares of their distances from the axis of rotation, or I = Σ mr 2. The first two wheels have, essentially, a uniform mass distribution, and the wheel on the right has most of its mass near the edge. The first one (on the left in the photograph) has a diameter of 2.5 inches (6.2 cm), and the other two have a diameter of 8.0 inches (20. You can invite interested students to come up after class to try spinning the wheels.Īll the wheels in this demonstration have a mass of 960 g. Seeing the difference in moments of inertia, but seeing how fast the wheels are spinning, and then how long each one takes to stop, gives a good sense of how an object’s moment of inertia affects its rotational dynamics. This demonstration is perhaps better for feeling rather than You twist the shaft of each one so that they all start at about the same rotational speed, the wheel with least moment of inertia stops rotating first, and the one with the greatest moment of inertia stops last. So that you can spin them by twisting the rods that run through their centers. Three wheels of equal mass but different moments of inertia are mounted


 0 kommentar(er)
0 kommentar(er)
